-
이진탐색(Binary Search) with Python알고리즘/문제풀이 2021. 1. 22. 21:29728x90
이진 탐색을 알아보기 전에 가장 기본 탐색 방법인 순차 탐색을 알아보고 이진 탐색을 알아본다.
1. 순차 탐색
순차 탐색은 리스트 안에 있는 특정 데이터를 찾기 위해서 앞에서부터 차례대로 확인하는 방법이다. 앞에서부터 하나씩 확인해야 하기 때문에 시간 복잡도는 O(N)이 된다.

단순 탐색 시간 복잡도 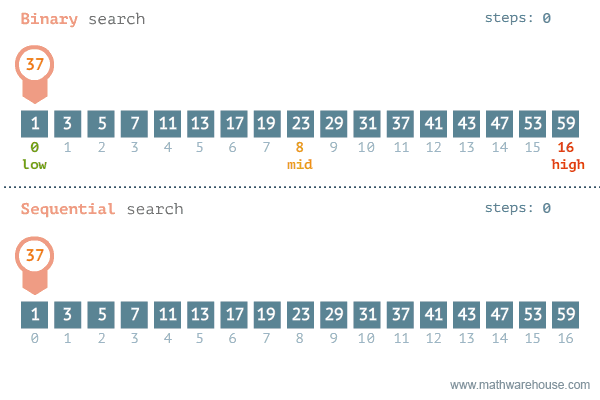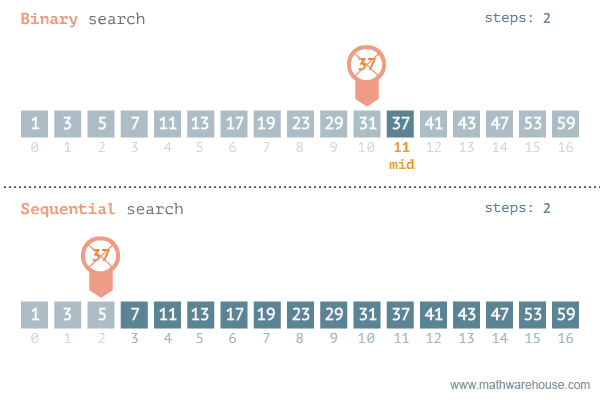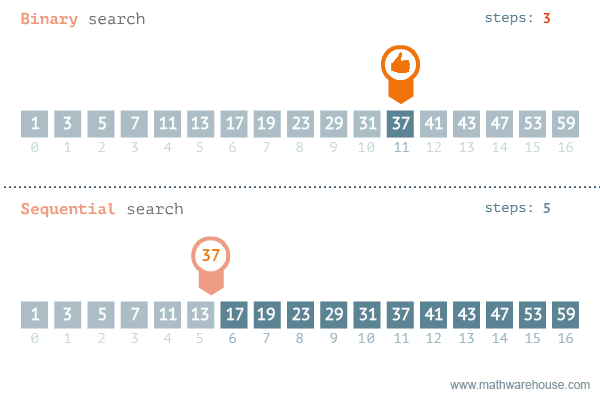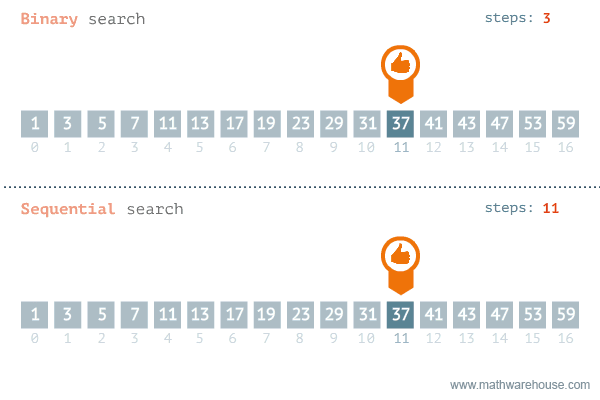
1-1. 구현하기
순차 탐색 소스를 구현하면 아래와 같다. 사람 이름 리스트 중 dongbin의 위치를 출력한다.
def sequential_search(n, target, array): for i in range(n): if array[i] == target: return i + 1 array = ["hanul", "jonggu", "dongbin", "taeil", "sangwook"] print(sequential_search(len(array), "dongbin", array)) # 3 출력
2. 이진 탐색(Binary Search)
이진 탐색이란 정렬된 배열에서 타겟을 찾는 검색 알고리즘으로 탐색 범위를 절반씩 좁혀가며 데이터를 탐색한다. 이는 이진 탐색 트리와 유사한 점이 많다. 그러나 이진 탐색 트리는 정렬된 구조를 저장하고 탐색하는 자료구조라면, 이진 탐색은 정렬된 배열에서 값을 찾는 알고리즘을 지칭한다.
이는 절반씩 좁혀서 탐색하기 때문에 시간 복잡도가 O(logN) 이다.

이진탐색 시간 복잡도 2-1. 이진 탐색 과정
이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.
아래는 10개의 데이터 중에 4인 원소를 찾는 과정이다. 이진 탐색을 이용하여 총 3번의 탐색으로 원소를 찾을 수 있다.

이진 탐색 과정 2-2. 구현하기
2-2-1. 재귀 함수 구현
def binary_search(array=list(), target=int(), left=int(), right=int()): """ 이진 탐색 - 재귀 함수 구현 :param array: 배열 :param target: 찾고자 하는 값 :param left: 왼쪽 인덱스 :param right: 오른쪽 인덱스 :return: target index """ if left > right: return None mid = (left + right) // 2 # 중간값. 몫 if target == array[mid]: return mid elif target > array[mid]: return binary_search(array=array, target=target, left=mid + 1, right=right) else: return binary_search(array=array, target=target, left=left, right=mid - 1) array=[-1, 0 , 3, 5, 9, 12] # 정렬된 리스트! result = binary_search(array=array, target=9, left=0, right=len(array) - 1) if result: print(result) else: print("없다")2-2-2. 반복문 구현
def binary_search(array=list(), target=int()): """ 이진 탐색 - 반복문 :param array: 배열 :param target: 찾고자 하는 값 :return: target index(찾고자 하는 값 인덱스) """ left = 0 right = len(array) - 1 while left <= right: mid = (left + right) // 2 if array[mid] == target: return mid elif array[mid] > target: right = mid -1 else: left = mid + 1 return None array=[-1, 0 , 3, 5, 9, 12] result = binary_search(array=array, target=9) if result: print(result) else: print("없다")2-2-3. 이진 탐색 모듈 사용
bisect 모듈은 이진 탐색 모듈이다. 자주 사용되는 메서드는 아래와 같다. bisect 메소드는 bisect_right와 동일하다.
만약 bisect_left(a, x)와 bisect_right(a, x)가 동일한 값이 나오면 target 값이 없는 것이다.

메소드 설명 bisect_left(a, x) 정렬된 a에 x를 삽입할 위치를 리턴한다. x가 이미 있는 경우는 x의 위치를 반환한다. bisect_right(a, x) 정렬된 a에 x를 삽입할 위치를 리턴한다. x가 이미 있는 경우는 오른쪽(뒤)의 인덱스를 리턴한다. - 예시
from bisect import bisect_left, bisect_right a = [1, 2, 4, 4, 8] target = 4 print(bisect_left(a, target)) # 2 print(bisect_right(a, target)) # 4- 이진 탐색 구하는 함수
import bisect def binary_search(array=list(), target=int()): """ 이진 탐색 - bisect :param array: :param target: :return: target index """ index = bisect.bisect_left(array, target) if index < len(array) and array[index] == target: return index return None array=[-1, 0, 3, 5, 9, 12] print(binary_search(array=array, target=9))- 범위를 구하는 함수
from bisect import bisect_left, bisect_right def count_by_range(a, left_value, right_value): right_value = bisect_right(a, right_value) left_value = bisect_left(a, left_value) return right_value - left_value a = [1, 2, 3, 3, 3, 3, 4, 4, 8, 9] print(count_by_range(a, 4, 4)) # 2 print(count_by_range(a, -1, 3)) # 6
3. 단순 탐색과 이진 탐색 비교
탐색 종류 단순 탐색 이진 탐색 의미 순서대로 추측한 것 중간을 탐색해서 비교해서 추측하는 것 예시 "lena"를 전화번호에서 찾기 위해 처음부터 찾는 경우 "lena"를 전화번호에서 찾기 위해 중간부터 찾는 경우 빅오표기법 O(n) O(logn) 특징 정렬 여부와 무관하다. 무조건 정렬이 되어 있어야 사용 가능하다.
4. 이진 탐색 문제 접근법
이진 탐색은 파라메트릭 서치 문제로 출제되는 경우가 많다.
파라메트릭 서치는 최적화 문제를 결정하는 문제(결정 문제: 예 혹은 아니오로 답하는 문제)로 바꾸어 해결하는 기법이다. 예를 들어 특정한 조건을 만족하는 가장 큰 값을 찾으라는 최적화 문제라면 이진 탐색을 이용해 해결할 수 있다.
5. 이진 탐색 트리
이진 탐색 트리란 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조이다. 이진 탐색 트리 자료구조를 구현하도록 요구하는 문제는 출제 빈도가 낮다. 따라서 간단히 데이터를 조회하는 과정만 살펴본다.
5-1. 트리 자료구조
이진트리구조를 살펴보기 전에 트리 자료구조를 살펴보자. 트리 자료구조는 아래와 같은 특징을 가지고 있다.
- 부모 노드와 자식 노드 관계로 표현된다.
- 최상단 노드를 루트 노드라고 한다.
- 최하단 노드를 단말 노드라고 한다.
- 트리에서 일부를 떼어내도 트리 구조이며 리를 서브 트리라 한다.
- 트리는 파일 시스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.

트리 자료구조 5-2. 이진 트리 특징
- 트리의 종류로 각 노드가 최대 2개의 자식 노드를 갖는 트리를 말한다.
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드

이진 트리 특징 5-3. 이진 탐색 트리 조회 과정
이진 탐색 트리에서 37 값을 가진 원소를 찾는 과정을 살펴보자.
step 1. 루트 노드 탐색
루트 노드부터 방문한다. 루트 노드는 30이다. 찾는 노드는 이보다 크니 오른쪽 트리만 탐색하도록 한다.

step 2. 오른쪽 노드 탐색
오른쪽 자식 노드인 48은 37보다 크다. 따라서 왼쪽 자식 노드를 탐색해야 한다.

step 3. 왼쪽 노드 탐색
현재 방문한 노드의 값이 37로 찾는 원소 값인 37과 동일하다. 따라서 탐색을 마친다.

참고
- 이것이 취업을 위한 코딩 테스트다 with 파이썬. 나동빈 저
반응형'알고리즘 > 문제풀이' 카테고리의 다른 글
[Python] 스타트 링크 5014 - bfs 그래프 탐색 (0) 2021.07.03 [Python] 백준 한 줄로 서기 1138 - 구현 문제 (0) 2021.07.03 [Python] programmers 메뉴 리뉴얼 - 구현 문제 (0) 2021.07.03 해시 알고리즘 (0) 2020.09.20 python 해시 테이블 (0) 2020.09.20
