해시 알고리즘

 이번 시간에는 해시 알고리즘에 대해서 알아본다. 해시 테이블과 해시 테이블에서 충돌이 발생하는 경우 해결방법 2가지를 알아본다. 

1. Direct Addressing Table

크기가 U인 테이블 T를 생성하고 key k를 slot key에 저장하는 방식이다. 해당 테이블은 중복되는 키가 없다고 가정한다. 이는 삽입, 삭제, 검색 모두 O(1)이지만, 모든 키를 넣어야 하기 때문에 공간 낭비가 심하다. 예를 들어 모든 학생들에게 한 자리씩 할당해 준 것이다.

Direct Addressing Table

---

2. Hash Table

 key k를 저장할 때 slot k를 저장하는 것이 아니라 slot h(k)에 저장한다. key k가 slot h(k)로 해시되었다고 하며, h(k)를 key k의 해시값이라고 부른다. 이때 h( )는 해시 함수라고 부른다.

 Hash Table은 Direct Addressing Table와 다르게 U 만큼의 테이블을 생성하지 않아도 되어 공간 낭비는 줄인다. 그러나 충돌 문제가 있다. 아래 그림에서는 h(k2) = h(k5) 부분이 충돌이 났다.

 시간 복잡도는 삽입, 삭제, 검색 모두 O(1) 이다.

Hash Table

2-1. Hash Table 용어

2-1-1. 충돌

두 개의 다른 key가 동일한 hash 값을 갖는 경우 "충돌이 발생했다"라고 한다. 충돌을 피하는 방법은 충돌이 적은 좋은 해시 함수를 사용하는 것이다. 아래에서 충돌을 해결하기 위한 Chaining과 Open Addressing 두 가지 방법을 알아보자.

2-1-2. 로드 팩터

로드 팩터란 해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다. 로드 팩터의 비율에 따라서 해시 함수를 재작성해야 될지 또는 해시 테이블 크기를 조정해야 할지를 결정한다. 자바 10에서는 해시 맵 디폴트 로드 팩터를 0.75로 정하여 이를 넘는 경우 해시 테이블의 공간을 재할당한다.

load factor = n/k

2-2. 좋은 해시 함수

좋은 해시 함수는 simple uniform hashing을 만족하는 함수이다. 이는 중복이 없이 확률적으로 슬롯에 골고루 나눠지는 것이다.

2-3. 해시 함수 종류

• 나눗셈 방법
  • 해쉬 함수로 나눗셈을 이용하는 방법으로 키 값 k를 m으로 나누고 나머지를 이용한다.
  • h(k) = k mod m

---

3. Chaining

Chaining

중복된 해시 값이 있는 경우, 해당 슬롯을 연결 리스트로 저장한다. 이 방법은 연결 리스트로 인해 최악의 경우 수행 시간이 O(n)이 된다. 해시를 사용하는 이유는 O(1)이라는 장점으로 사용하는 것인데 O(n)이 된다면 문제가 된다.

---

4. Open Addressing

오픈 어드레싱은 충돌을 피하기 위한 다른 방법으로 key를 해시 테이블에 직접 저장한다. 오픈 어드레싱의 장점은 포인터를 사용하지 않아도 되어 구현이 간편하며, 검색도 미세하게 빨라진다.

오픈 어드레싱은 총 3가지 종류가 있다. 각 종류의 특징을 알아보도록 하자.

4-1. 선형 프로빙(Linear probing)

선형 프로빙은 충돌이 발생할 경우 빈 slot이 나올 때까지 탐색 후, 빈 slot이 나오면 위치가 결정된다. 선형 프로빙은 아래와 같은 해시 함수가 사용된다. 여기서 k는 키, i는 충돌 횟수, h()는 해시 함수를 의미한다.

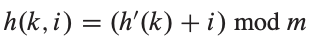
4-1-1. 해시 삽입

 아래는 선형 프로빙에서 키를 삽입하는 수도 코드이다. NIL이 있으면 넣고, 아닌 경우 다음 칸으로 이동하는 것을 확인할 수 있다.

4-1-2. 해시 검색

아래는 선형 프로빙에서 키를 검색하는 수도 코드이다. NIL이 아닐 때까지 계속 다음 칸으로 이동하면서 검색하는 것을 확인할 수 있다.

4-1-3. 해시 삭제

값을 지우는 경우는 해당 slot에 "DELETED"라고 표시해야 한다. 왜냐하면 검색할 때 빈 slot이 있을 때까지 검색하기 때문에 빈 값으로 두면 그 이후를 검색이 안 되는 경우가 발생합니다. 따라서 "DELETED"와 같은 특정 값을 넣어 줘야 검색 시 문제가 없습니다.

4-1-4. 장단점

선형 프로빙의 장점은 구현은 매우 쉬우나 primary clustering 문제가 있다. primary clustering는 한 번 충돌이 나면 집중적으로 충돌이 발생하는 것을 의미한다. 이로 인하여 평균 검색 시간이 증가한다.

 

4-2. 이차식 프로빙(Quadratic probing)

이차식 프로빙은 아래와 같은 해시 함수를 사용한다. i에 대한 2차 함수 꼴로 slot를 이동하면서 빈 slot를 찾는다.

• h: 보조 해시 함수
• c1, c2: 0이 아닌 상수

4-2-1. 장단점

이차식 프로빙은 선형 프로빙에 비해 충돌이 적지만 secondary clustering이 발생한다. secondary clustering은 처음 충돌한 위치가 같다면 다음 충돌할 위치도 반복적으로 계속 충돌이 나게 된다는 의미이다.

4-3. 이중 해시(Double hasing)

이중 해시는 다음과 같은 형태의 해시 함수를 사용한다. 충돌이 없을 때는 h1으로 위치를 탐색하고, 충돌이 있으면 h2 mod m 만큼 이동하면서 탐색한다.

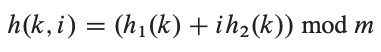
4-3-1. 주의점

이중 해시는 h2(k) 함수는 해시 테이블 크기 m과 서로소 관계로 해야 한다.

---

참고 내용 

• Introduction to Algorithms - 3rd Edition